Skip to main content

Mirror image of Binary tree

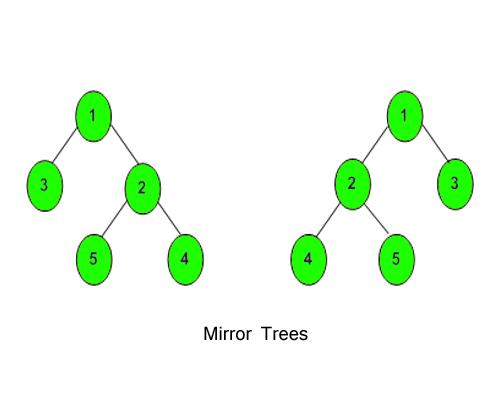
 Given a Binary Tree, convert it into its mirror.

MirrorTree1            

Example 1:

Input:
      1
    /  \
   2    3
Output: 3 1 2
Explanation: The tree is
   1    (mirror)  1
 /  \    =>      /  \
2    3          3    2
The inorder of mirror is 3 1 2

Example 2:

Input:
      10
     /  \
    20   30
   /  \
  40  60
Output: 30 10 60 20 40
Explanation: The tree is
      10               10
    /    \  (mirror) /    \
   20    30    =>   30    20
  /  \                   /   \
 40  60                 60   40
The inroder traversal of mirror is
30 10 60 20 40.

Your Task:
Just complete the function mirror() that takes node as paramter  and convert it into its mirror. The printing is done by the driver code only.

Expected Time Complexity: O(N).
Expected Auxiliary Space: O(Height of the Tree).

Constraints:
1 ≤ Number of nodes ≤ 105
1 ≤ Data of a node ≤ 105








Ans :




void swapNode(Node *a , Node *b)

{

    Node *c ;

    c = a;

    a = b ;

    b = c;

}



class Solution {

  public:

    // Function to convert a binary tree into its mirror tree.

    void mirror(Node* node) {

        

        queue<Node *> q;

        q.push(node);

        while(!q.empty())

        {

            if(q.front()->left)

            q.push(q.front()->left);

            if(q.front()->right)

            q.push(q.front()->right);

            swap(q.front()->left , q.front()->right );

            q.pop();

        }

    }

};




Refrences : https://practice.geeksforgeeks.org/problems/mirror-tree/1#

Labels:

Comments

Post a Comment

Popular posts from this blog

[PDF DOWNLOAD] AKTU Quantum series data structure b.tech 2nd year download

  All AKTU Quantums are available here. Get your hands on AKTU Quantums and boost your grades in AKTU semester exams. You can either search them category wise or can use the search bar or can manually search on this page. Download aktu second year quantum pdf data structures  download  data structures quantum aktu download aktu data structures quantum click here to download  write in comment section if you want quantum of any other subject.
Post a Comment
Read more

2485. Find the Pivot Integer | Binary search

  Given a positive integer   n , find the   pivot integer   x   such that: The sum of all elements between  1  and  x  inclusively equals the sum of all elements between  x  and  n  inclusively. Return  the pivot integer  x . If no such integer exists, return  -1 . It is guaranteed that there will be at most one pivot index for the given input.   Example 1: Input: n = 8 Output: 6 Explanation: 6 is the pivot integer since: 1 + 2 + 3 + 4 + 5 + 6 = 6 + 7 + 8 = 21. Example 2: Input: n = 1 Output: 1 Explanation: 1 is the pivot integer since: 1 = 1. Example 3: Input: n = 4 Output: -1 Explanation: It can be proved that no such integer exist.   Constraints: 1 <= n <= 1000 Solution : class Solution { publ ic:     int pivotInteger( int n ) {         int sum = (( n )*( n + 1 ))/ 2 ;         int i = 1 ;         int j =...
Post a Comment
Read more

leetcode 48 solution

  48 .  Rotate Image You are given an  n x n  2D  matrix  representing an image, rotate the image by  90  degrees (clockwise). You have to rotate the image  in-place , which means you have to modify the input 2D matrix directly.  DO NOT  allocate another 2D matrix and do the rotation.   Example 1: Input: matrix = [[1,2,3],[4,5,6],[7,8,9]] Output: [[7,4,1],[8,5,2],[9,6,3]] Example 2: Input: matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]] Output: [[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]   Constraints: n == matrix.length == matrix[i].length 1 <= n <= 20 -1000 <= matrix[i][j] <= 1000 solution: class Solution { public:     void swap(int& a , int &b)     {         int c ;         c = a;         a = b;         b = c;     }     void transpose (vector<vector<int>...
Post a Comment
Read more