Skip to main content

image overlap | leetcode solution

835. Image Overlap

You are given two images, img1 and img2, represented as binary, square matrices of size n x n. A binary matrix has only 0s and 1s as values.

We translate one image however we choose by sliding all the 1 bits left, right, up, and/or down any number of units. We then place it on top of the other image. We can then calculate the overlap by counting the number of positions that have a 1 in both images.

Note also that a translation does not include any kind of rotation. Any 1 bits that are translated outside of the matrix borders are erased.

Return the largest possible overlap.

 

Example 1:

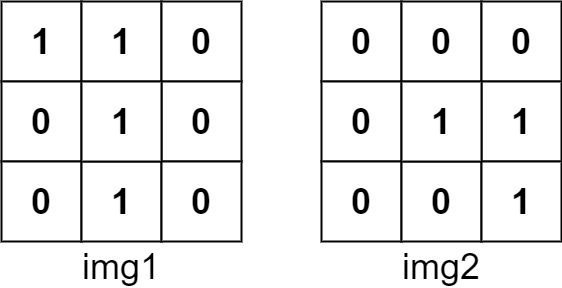
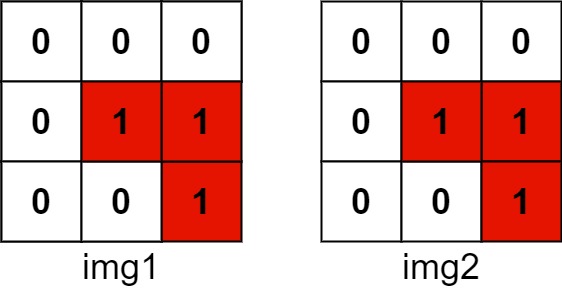
Input: img1 = [[1,1,0],[0,1,0],[0,1,0]], img2 = [[0,0,0],[0,1,1],[0,0,1]]
Output: 3
Explanation: We translate img1 to right by 1 unit and down by 1 unit.

The number of positions that have a 1 in both images is 3 (shown in red).

Example 2:

Input: img1 = [[1]], img2 = [[1]]
Output: 1

Example 3:

Input: img1 = [[0]], img2 = [[0]]
Output: 0

 

Constraints:

  • n == img1.length == img1[i].length
  • n == img2.length == img2[i].length
  • 1 <= n <= 30
  • img1[i][j] is either 0 or 1.
  • img2[i][j] is either 0 or 1.

solution:

class Solution {
public:
    int largestOverlap(vector<vector<int>>& img1, vector<vector<int>>& img2) {
        int n=img1.size();
        vector<pair<int,int>>vec_a;
        vector<pair<int,int>>vec_b;
        for(int i=0;i<n;i++){
            for(int j=0;j<n;j++){
                if(img1[i][j]==1){
                    vec_a.push_back({i,j});
                }
                if(img2[i][j]==1){
                    vec_b.push_back({i,j});
                }
            }
        }
        int ans=0;
        map<pair<int,int>,int>mp;
        for(auto [i1,j1]:vec_a){
            for(auto [i2,j2]:vec_b){
                mp[{i1-i2,j1-j2}]++;
                ans=max(ans,mp[{i1-i2,j1-j2}]);
            }
        }
        return ans;
    }
};

 

Labels:

Comments

Post a Comment

Popular posts from this blog

leetcode 48 solution

  48 .  Rotate Image You are given an  n x n  2D  matrix  representing an image, rotate the image by  90  degrees (clockwise). You have to rotate the image  in-place , which means you have to modify the input 2D matrix directly.  DO NOT  allocate another 2D matrix and do the rotation.   Example 1: Input: matrix = [[1,2,3],[4,5,6],[7,8,9]] Output: [[7,4,1],[8,5,2],[9,6,3]] Example 2: Input: matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]] Output: [[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]   Constraints: n == matrix.length == matrix[i].length 1 <= n <= 20 -1000 <= matrix[i][j] <= 1000 solution: class Solution { public:     void swap(int& a , int &b)     {         int c ;         c = a;         a = b;         b = c;     }     void transpose (vector<vector<int>...
Post a Comment
Read more

Regular Expression Matching Leetcode Solution

Regular Expression Matching Given an input string s and a pattern p, implement regular expression matching with support for '.' and '*' where: '.' Matches any single character.​​​​ '*' Matches zero or more of the preceding element. The matching should cover the entire input string (not partial). Example 1: Input: s = "aa", p = "a"  Output: false  Explanation: "a" does not match the entire string "aa". Example 2: Input: s = "aa", p = "a*"  Output: true  Explanation: '*' means zero or more of the preceding element, 'a'. Therefore, by repeating 'a' once, it becomes "aa". Example 3: Input: s = "ab", p = ".*"  Output: true  Explanation: ".*" means "zero or more (*) of any character (.)". Constraints: 1 <= s.length <= 20 1 <= p.length <= 20 s contains only lowercase English letters. p contains only lowercase Englis...
Post a Comment
Read more

2485. Find the Pivot Integer | Binary search

  Given a positive integer   n , find the   pivot integer   x   such that: The sum of all elements between  1  and  x  inclusively equals the sum of all elements between  x  and  n  inclusively. Return  the pivot integer  x . If no such integer exists, return  -1 . It is guaranteed that there will be at most one pivot index for the given input.   Example 1: Input: n = 8 Output: 6 Explanation: 6 is the pivot integer since: 1 + 2 + 3 + 4 + 5 + 6 = 6 + 7 + 8 = 21. Example 2: Input: n = 1 Output: 1 Explanation: 1 is the pivot integer since: 1 = 1. Example 3: Input: n = 4 Output: -1 Explanation: It can be proved that no such integer exist.   Constraints: 1 <= n <= 1000 Solution : class Solution { publ ic:     int pivotInteger( int n ) {         int sum = (( n )*( n + 1 ))/ 2 ;         int i = 1 ;         int j =...
Post a Comment
Read more